机械同感

本篇一部分翻译自Go and CPU Caches - Teiva Harsanyi - Medium，和 【译】CPU 高速缓存原理和应用 - 云+社区 - 腾讯云。

其中代码部分亲自做了基准测试，和作者的有出入，本文会加入我的解释。

很早很早以前，面试过一个同学，他说他对底层非常感兴趣，看过很多底层设计的书，我问他说这些对日常的工作有什么帮助吗，他说每天的工作就是CURD，底层知识几乎用不到，所以很苦恼。

这里想解释一个词，叫机械同感 (Mechanical Sympathy)。

曾三次获得 F1 世界冠军的杰基* 斯图尔特 (Jackie Stewart) 表示，了解汽车的工作原理让他成为了一名更好的驾驶员。

“你并不需要先成为一个工程师才能去做一个赛车手，但是你得有一种机械同感”。

简而言之，了解计算机底层硬件能让我们作为一个更优秀的开发者去设计算法、数据结构等等。

CPU 高速缓存基本原理

现代计算机处理器是基于一种叫对称多处理 (symmetric multiprocessing, SMP) 的概念。在一个 SMP 系统里，处理器的设计使两个或多个核心连接到一片共享内存 (也叫做主存，RAM)。另外，为了加速内存访问，处理器有着不同级别的缓存，分别是 L1、L2 和 L3。确切的体系结构可能因供应商、处理器模型等等而异。然而，目前最流行的模型是把 L1 和 L2 缓存内嵌在 CPU 核心本地，而把 L3 缓存设计成跨核心共享：

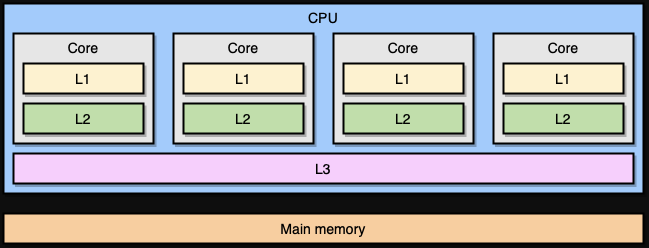
越靠近 CPU 核心的缓存，容量就越小，同时访问延迟就越低 (越快)：

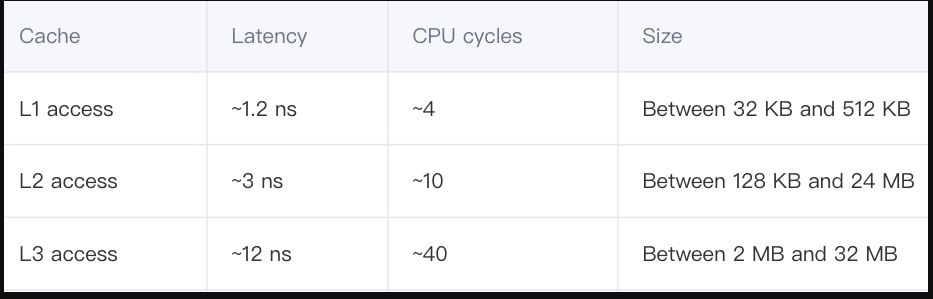
同样的，这些具体的数字因不同的处理器模型而异。不过，我们可以做一个粗略的估算：假设 CPU 访问主存需要耗费 60 ns，那么访问 L1 缓存会快上 50 倍。

在处理器的世界里，有一个很重要的概念叫访问局部性 (locality of reference)，当处理器访问某个特定的内存地址时，有很大的概率会发生下面的情况：

• CPU 在不久的将来会去访问相同的地址：这叫 时间局部性 (temporal locality) 原则。
• CPU 会访问特定地址附近的内存地址：这叫 空间局部性 (spatial locality) 原则。

之所以会有 CPU 缓存，时间局部性是其中一个重要的原因。不过，我们到底应该怎么利用处理器的空间局部性呢？比起拷贝一个单独的内存地址到 CPU 缓存里，拷贝一个 缓存行 (Cache Line) 是更好的实现。一个缓存行是一个连续的内存段。缓存行的大小取决于缓存的级别 (同样的，具体还是取决于处理器模型)。举个例子，这是我的电脑的 L1 缓存行的大小：

$ sysctl -a | grep cacheline
hw.cachelinesize: 64

处理器会拷贝一段连续的 64 字节的内存段到 L1 缓存里，而不是仅仅拷贝一个单独的变量。举个例子，当处理器要拷贝一个由 int64 类型组成 Go 的切片到 CPU 缓存里的时候，它会一起拷贝 8 个元素，而不是单单拷贝 1 个。

一个具体应用缓存行的 Go 程序

让我们来看一个具体的例子，这个例子将会给我们展示利用 CPU 缓存带来的好处。下面的代码完成的功能是合并两个由 int64 类型组成的方形矩阵： (这里用到了GO自带的基准压测)

func BenchmarkMatrixCombination(b *testing.B) {
 matrixA := createMatrix(matrixLength)
 matrixB := createMatrix(matrixLength)

 for n := 0; n < b.N; n++ {
  for i := 0; i < matrixLength; i++ {
   for j := 0; j < matrixLength; j++ {
    matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
   }
  }
 }
}

给定的 matrixLength 变量值设为 6400，压测结果如下：

BenchmarkMatrixCombination-4                   	       1	1493128112 ns/op

现在，我们把加 matrixB[I][j] 的操作换成 matrixB[j][I] ：

func BenchmarkMatrixReversedCombination(b *testing.B) {
 matrixA := createMatrix(matrixLength)
 matrixB := createMatrix(matrixLength)

 for n := 0; n < b.N; n++ {
  for i := 0; i < matrixLength; i++ {
   for j := 0; j < matrixLength; j++ {
    matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
   }
  }
 }
}

改动之后对压测结果的影响有多大呢？

BenchmarkMatrixCombination-4                   	       1	1493128112 ns/op
BenchmarkMatrixReversedCombination-4           	       1	2430968823 ns/op

性能下降了！那该怎么解释这个结果呢？

让我们画几幅图来更直观地描述一下中间到底发生了什么，蓝色圆圈代表第一个矩阵的当前指针而粉红色圆圈代表了第二个矩阵的指针。由于程序的操作是 matrixA[i][j] = matrixA[i][j] + matrixB[j][i] ，所以当蓝色指针处于坐标 (4,0) 之时，粉红色指针对应的坐标就是 (0,4)：

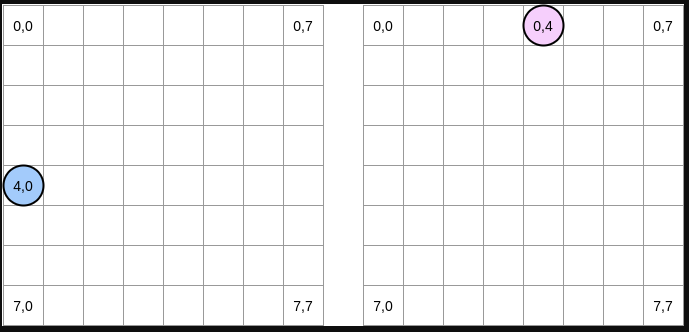
在上面的图解中，我们用横坐标纵坐标来表示矩阵，(0,0) 代表顶上最左的方块。从计算机原理的角度，一个矩阵所有的行将会被分配到一片连续的内存上，不过为了更直观地表示，我们还是按照数学的表示方法。

此外，接下来的例子里，矩阵的大小是缓存行大小的倍数。因此，一个缓存行不会在下一个矩阵行溢出。 程序会怎么遍历矩阵？蓝色指针会一直向右移动直到最后一列，然后移到下一行，到达坐标 (5,0)，以此类推。相反地，粉红色指针会一直往下移动直到最后一行，然后移到下一列。当粉红色指针在坐标 (0,4) 之时，处理器会缓存指针所在那一行 (在这个示意图里，我们假设缓存行的大小是 4 个元素)：

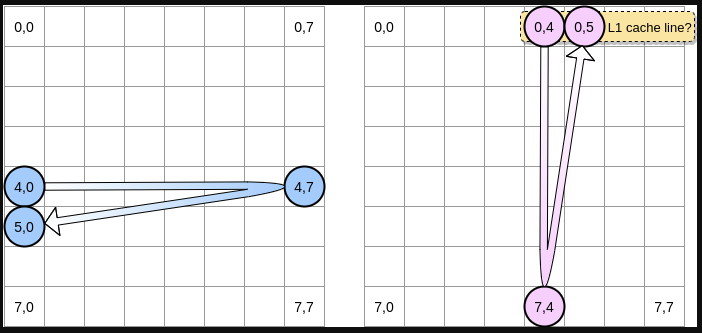
因此，当粉红色指针到达坐标 (0,5) 之时，我们可能会假定这个变量已经在 L1 缓存里了对不对？实际上这取决于矩阵的大小：

• 如果矩阵足够小从而所有的缓存行都能被容纳在 L1 里，那答案就是肯定的。
• 否则的话，该缓存行就会在指针达到 (0,5) 之前就被清出 L1。因此，将会产生一个缓存缺失，然后处理器就不得不通过别的方式访问该变量 (比如从 L2 里去取)。此时，程序的状态将会是这样的：

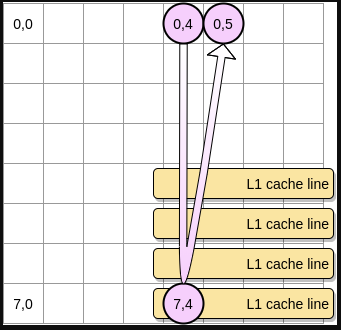
所以按这个推理， matrixA[i][j] = matrixA[i][j] + matrixB[i][j] 改成 matrixA[i][j] = matrixA[j][i] + matrixB[j][i] 后性能会继续下降。

BenchmarkMatrixCombination-4                           1	1493128112 ns/op
BenchmarkMatrixReversedCombination-4                   1	2430968823 ns/op
BenchmarkMatrixReversedCombination2-4                  1	2723984776 ns/op

那么矩阵的容量应该达到多小才能从 L1 缓存中获益呢？让我们做个简单的计算：首先，我们需要知道 L1 缓存的容量有多大：

$ sysctl hw.l1icachesize
hw.l1icachesize: 32768

在我的机器上，L1 缓存的大小是 32768 字节而缓存行的大小是 64 字节。因此，我最多能存 512 个缓存行到 L1 里。那么如果我们把上面的程序里的矩阵的大小改成 512 之后再跑一下压测，结果会怎样？

BenchmarkMatrixCombination-4                   	    1281	   1744384 ns/op
BenchmarkMatrixReversedCombination-4           	     898	   2650332 ns/op
BenchmarkMatrixReversedCombination2-4          	     144	   8341895 ns/op

尽管我们已经把两个测试用例的性能差距缩小了很多，我们还是可以看到会有细微的差距。到底是哪里出了问题？在压测过程中，我们使用了两个矩阵，因此 CPU 需要储存这两个矩阵的所有缓存行。在一个完全理想的状态下 (比如压测过程中没有其他程序在运行，而这几乎是不可能的)，L1 缓存会用 50% 的容量来存第一个矩阵而用另外的 50% 的容量来存第二个矩阵。那我们就再进一步缩小两个矩阵的大小，缩减到 256 个元素：

BenchmarkMatrixCombination-4                   	    2995	    653952 ns/op
BenchmarkMatrixReversedCombination-4           	    2154	    549830 ns/op
BenchmarkMatrixReversedCombination2-4          	    2865	    795512 ns/op

现在我们终于得到了一个近乎相等的压测结果了。

关于为什么第二个测试用例还要略微地比第一个快，这点差别看起来不是很容易察觉而且应该和 Go 编译器生成的汇编代码有关。在第二个测试用例里，第二个矩阵上的指针区别于第一个矩阵指针的管理方式，使用的是 LEA (Load Effective Address) 汇编指令。因为操作系统的虚拟内存机制，当一个处理器访问一个内存地址时，需要做一个虚拟内存到物理真实内存的转换。使用 LEA 指令允许你不经过虚拟内存的转换直接得到内存地址。举个例子，如果我们维护一个由 int64 类型元素组成的切片，我们已经知道了切片里第一个元素的地址，我们就能使用 LEA 指令简单地往后移动 8 个字节得到第二个元素的地址。在我们的例子里，这可能就是为什么第二个测试更快的原因。

好了，那我们现在怎么才能在处理一个大容量矩阵时减少处理器缓存缺失带来的影响呢？这里介绍一种叫 嵌套循环最优化 (Loop Nest Optimization)的技巧：我们遍历矩阵的时候，每次都以一个指定大小的矩阵块为单位来遍历，以此来最大化利用 CPU 缓存。

在上面的例子里定义一个包含 4 * 4 大小的矩阵块。在第一个矩阵里，我们从 (4,0) 到 (4,3) 遍历一次，然后切换到下一行。相应的，我们在第二个矩阵里就是从 (0,4) 到 (3,4) 遍历一次，然后切换到下一列。

当粉红色指针遍历完第一列之后，处理器就会把相应的的所有缓存行都储存到 L1 里了，因此，遍历剩下的那些元素的时候就都是从 L1 里访问了，这样就能加快速度了：

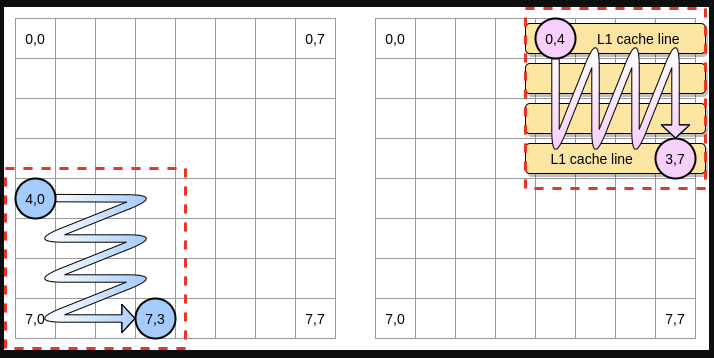
让我们把上述的思路用 Go 实现出来，不过我们得谨慎地选择矩阵块的大小。在之前的例子里，矩阵块的边长等于缓存行的大小，这个值不能设置得再小了，否则的话，缓存行里就会有空余，浪费空间。在我们的 Go 压测程序里，矩阵的元素是 int64 类型 (8 个字节)，而缓存行是 64 字节，可以储存 8 个元素，那么矩阵块的边长就至少要是 8：

func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B) {
 matrixA := createMatrix(matrixLength)
 matrixB := createMatrix(matrixLength)
 blockSize := 8

 for n := 0; n < b.N; n++ {
  for i := 0; i < matrixLength; i += blockSize {
   for j := 0; j < matrixLength; j += blockSize {
    for ii := i; ii < i+blockSize; ii++ {
     for jj := j; jj < j+blockSize; jj++ {
      matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
     }
    }
   }
  }
 }
}

现在用这个最新的代码实现去跑压测，以下是每种matrixLength的测试结果 matrixLength=6400

BenchmarkMatrixCombination-4                   	       1	1493128112 ns/op
BenchmarkMatrixReversedCombination-4           	       1	2430968823 ns/op
BenchmarkMatrixReversedCombination2-4          	       1	2723984776 ns/op
BenchmarkMatrixReversedCombinationPerBlock-4   	       4	 374949868 ns/op

matrixLength=512

BenchmarkMatrixCombination-4                   	    1281	   1744384 ns/op
BenchmarkMatrixReversedCombination-4           	     898	   2650332 ns/op
BenchmarkMatrixReversedCombination2-4          	     144	   8341895 ns/op
BenchmarkMatrixReversedCombinationPerBlock-4   	     740	   1392904 ns/op

matrixLength=256

BenchmarkMatrixCombination-4                   	    2995	    653952 ns/op
BenchmarkMatrixReversedCombination-4           	    2154	    549830 ns/op
BenchmarkMatrixReversedCombination2-4          	    2865	    795512 ns/op
BenchmarkMatrixReversedCombinationPerBlock-4   	    3790	    369770 ns/op

这就是用来展示对 CPU 缓存的了解可以如何潜在地帮助我们设计更高效算法的第一个例子。

伪共享 (False Sharing)

经过上面的分析，我们现在应该对处理器如何管理内部缓存有一个比较清晰的理解了；再来快速回顾一下：

• 因为空间局部性原则，处理器会储存缓存行而不是一个单独内存地址。
• L1 缓存是内嵌在指定的 CPU 核心本地的。

要真正理解伪共享，首先要了解 MESI 协议及 RFO 请求： 从前面的内容我们可以知道，每个核心都有自己私有的 L1、L2 缓存。那么多线程编程时， 另外一个核的线程想要访问当前核内 L1、L2 缓存行的数据， 该怎么做呢？

有人说可以通过第 2 个核直接访问第 1 个核的缓存行，这是当然是可行的，但这种方法不够快。跨核访问需要通过 Memory Controller (内存控制器，是计算机系统内部控制内存并且通过内存控制器使内存与 CPU 之间交换数据的重要组成部分），典型的情况是第 2 个核经常访问第 1 个核的这条数据，那么每次都有跨核的消耗。更糟的情况是，有可能第 2 个核与第 1 个核不在一个插槽内，况且 Memory Controller 的总线带宽是有限的，扛不住这么多数据传输。所以，CPU 设计者们更偏向于另一种办法：如果第 2 个核需要这份数据，由第 1 个核直接把数据内容发过去，数据只需要传一次。

那么什么时候会发生缓存行的传输呢？答案很简单：当一个核需要读取另外一个核的脏缓存行时发生。但是前者怎么判断后者的缓存行已经被弄脏(写)了呢？

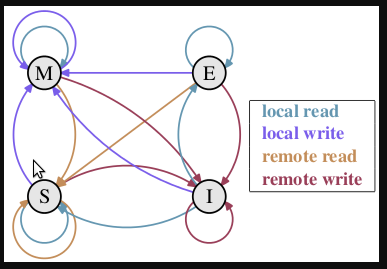
下面将详细地解答以上问题。首先我们需要谈到一个协议—— MESI 协议。现在主流的处理器都是用它来保证缓存的相干性和内存的相干性。M、E、S 和 I 代表使用 MESI 协议时缓存行所处的四个状态：

M（修改，Modified）：本地处理器已经修改缓存行，即是脏行，它的内容与内存中的内容不一样，并且此 cache 只有本地一个拷贝(专有)；

E（专有，Exclusive）：缓存行内容和内存中的一样，而且其它处理器都没有这行数据；

S（共享，Shared）：缓存行内容和内存中的一样, 有可能其它处理器也存在此缓存行的拷贝；

I（无效，Invalid）：缓存行失效, 不能使用。

下面说明这四个状态是如何转换的：

初始：一开始时，缓存行没有加载任何数据，所以它处于 I 状态。

本地写（Local Write）：如果本地处理器写数据至处于 I 状态的缓存行，则缓存行的状态变成 M。

本地读（Local Read）：如果本地处理器读取处于 I 状态的缓存行，很明显此缓存没有数据给它。此时分两种情况：(1)其它处理器的缓存里也没有此行数据，则从内存加载数据到此缓存行后，再将它设成 E 状态，表示只有我一家有这条数据，其它处理器都没有；(2)其它处理器的缓存有此行数据，则将此缓存行的状态设为 S 状态。（备注：如果处于M状态的缓存行，再由本地处理器写入/读出，状态是不会改变的）

远程读（Remote Read）：假设我们有两个处理器 c1 和 c2，如果 c2 需要读另外一个处理器 c1 的缓存行内容，c1 需要把它缓存行的内容通过内存控制器 (Memory Controller) 发送给 c2，c2 接到后将相应的缓存行状态设为 S。在设置之前，内存也得从总线上得到这份数据并保存。

远程写（Remote Write）：其实确切地说不是远程写，而是 c2 得到 c1 的数据后，不是为了读，而是为了写。也算是本地写，只是 c1 也拥有这份数据的拷贝，这该怎么办呢？c2 将发出一个 RFO (Request For Owner) 请求，它需要拥有这行数据的权限，其它处理器的相应缓存行设为 I，除了它自已，谁不能动这行数据。这保证了数据的安全，同时处理 RFO 请求以及设置I的过程将给写操作带来很大的性能消耗。

下面添加一个简单的 MESI 状态转换图：

现在，让我们通过一个例子来讨论一下 L1 缓存一致性和伪共享的问题。假设现在有两个变量：var1 和 var2 被储存在主存里，一个在 core1 里的线程访问 var1 ，而另一个 core2 里的线程访问 var2 。假设这两个变量在内存中的位置是相邻的 (或者是非常靠近的)，那么最后就会导致 var2 存在于两个核心的同一个 L1 缓存行里：

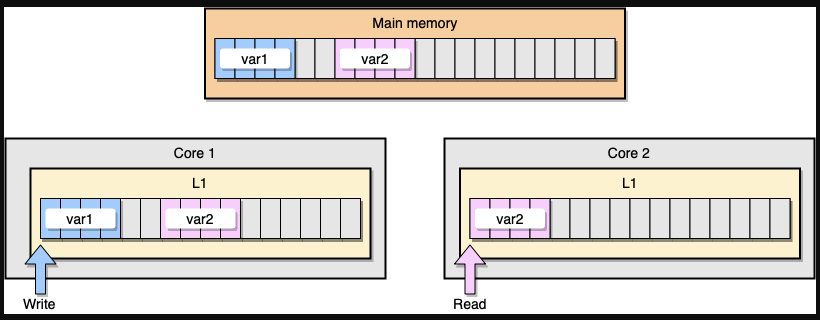
上图中 thread1 位于 core1 ，而 thread2 位于 core2 ，二者均想更新彼此独立的两个变量，但是由于两个变量位于不同核心中的同一个 L1 缓存行中，此时可知的是两个缓存行的状态应该都是 Shared ，而对于同一个缓存行的操作，不同的 core 间必须通过发送 RFO 消息来争夺所有权 (ownership) ，如果 core1 抢到了， thread1 因此去更新该缓存行，把状态变成 Modified ，那就会导致 core2 中对应的缓存行失效变成 Invalid ，当 thread2 取得所有权之后再去更新该缓存行时必须先让 core1 把对应的缓存行刷回 L3 缓存/主存，然后它再从 L3 缓存/主存中加载该缓存行进 L1 之后才能进行修改。然而，这个过程又会导致 core1 对应的缓存行失效变成 Invalid ，这个过程将会一直循环发生，从而导致 L1 高速缓存并未起到应有的作用，反而会降低性能；轮番夺取所有权不但带来大量的 RFO 消息，而且如果某个线程需要读此行数据时，L1 和 L2 缓存上都是失效数据，只有 L3 缓存上是同步好的数据，而从前面的内容可以知道，L3 的读取速度相比 L1/L2 要慢了数十倍，性能下降很大；更坏的情况是跨槽读取，L3 都不能命中，只能从主存上加载，那就更慢了。

请记住，CPU 缓存的最小的处理单位永远是缓存行 (Cache Line)，所以当某个核心发送 RFO 消息请求把其他核心对应的缓存行设置成Invalid 从而使得 var1 缓存失效的同时，也会导致同在一个缓存行里的 var2 失效，反之亦然。

我们来看一个具体的 Go 程序。在这个例子里，我们相继地实例化了两个结构体，一个紧挨着另一个；因此，这两个结构体应该会被分配在一片连续的内存上；然后，我们再创建两个 goroutines，分别去访问对应的结构体 (变量 M 的值等于 100 万)：

type SimpleStruct struct {
 n int
}

func BenchmarkStructureFalseSharing(b *testing.B) {
 structA := SimpleStruct{}
 structB := SimpleStruct{}
 wg := sync.WaitGroup{}

 b.ResetTimer()
 for i := 0; i < b.N; i++ {
  wg.Add(2)
  go func() {
   for j := 0; j < M; j++ {
    structA.n += j
   }
   wg.Done()
  }()
  go func() {
   for j := 0; j < M; j++ {
    structB.n += j
   }
   wg.Done()
  }()
  wg.Wait()
 }
}

在这个例子里，第二个结构体里的变量 n 只会被第二个 goroutine 访问，然而，因为两个结构体在内存上的地址是连续的， n 将会存在于两个 CPU 缓存行中 (这里假设两个 goroutine 会被分配到不同核心上调度，当然，这通常不是必须的)，这是压测结果：

BenchmarkStructureFalseSharing-4   	     152	   7578517 ns/op

那么我们如何才能规避这种伪共享呢？有一个解决办法是使用内存填充 (memory padding)。这种方案的原理是在两个变量之间填充足够多的空间，以确保它们会储存在不同的 CPU 缓存行里。

首先，让我们创建一个替代之前那个结构体的新结构体，在变量声明之后填充足够的内存：

type PaddedStruct struct {
 n int
 _ CacheLinePad
}

type CacheLinePad struct {
 _ [CacheLinePadSize]byte
}

const CacheLinePadSize = 64

接着，我们再初始化这两个结构体而且和之前一样通过单独的 goroutine 分别去访问这两个变量：

func BenchmarkStructurePadding(b *testing.B) {
 structA := PaddedStruct{}
 structB := SimpleStruct{}
 wg := sync.WaitGroup{}

 b.ResetTimer()
 for i := 0; i < b.N; i++ {
  wg.Add(2)
  go func() {
   for j := 0; j < M; j++ {
    structA.n += j
   }
   wg.Done()
  }()
  go func() {
   for j := 0; j < M; j++ {
    structB.n += j
   }
   wg.Done()
  }()
  wg.Wait()
 }
}

内存智能化，这个例子里的内存分布应该看起来像下图这样，两个变量之间留有足够多的内存填充，从而导致它们最后只会分别存在于不同核心的缓存行上：

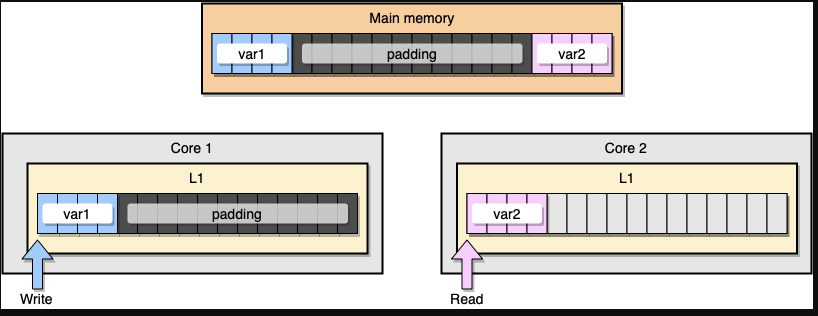
让我们来看下最新的压测结果：

BenchmarkStructureFalseSharing-4   	     152	   7578517 ns/op
BenchmarkStructurePadding-4        	     351	   4304213 ns/op

使用了内存填充之后的第二个例子要比最初的那个快了差不多 40% ?，虽然不是没有代价的。内存填充的确能加快执行时间，不过代价是会导致更多的内存分配和浪费。